En este y en los siguientes tutoriales, aprenderás los fundamentos del Aprendizaje Automático usando Python. En este tutorial, se explicará la regresión lineal. Antes de empezar a codificar, ¿qué es la regresión lineal? Bueno, la regresión lineal es un algoritmo donde los valores predichos tienen una pendiente lineal. En general, la regresión se utiliza sobre todo para encontrar la relación entre las variables y la predicción. En el caso de la regresión lineal, esta relación será lineal.

En este tutorial, la regresión lineal se realizará utilizando la multiplicación de matrices. Si recordamos nuestras lecciones de Matemáticas del colegio, una relación lineal entre las variables dependiente e independiente tiene la forma \[y = c_{0}*x^{0} + c_{1}*x^{1}\] ó \[y = c_{0} + c_{1}*x\], donde $c_0$ es la intercepción con el eje $y$, y $c_1$ - la pendiente de la recta.

Esta relación se puede expresar de forma matricial. En el sistema tendremos 3 matrices. La primera serán los valores de $y$, la segunda será un conjunto de $x$ (en este caso sólo tendremos $x_0$ y $x_1$) conocida como matriz de Vandermonde, y la tercera matriz estará formada por los coeficientes de $x$.

Dicho esto, ¡comencemos a codificar en Python! Para este tutorial, los valores de $y$ y $x$ están en un archivo de texto llamado 'points.txt' guardado en el mismo directorio que su archivo de Python. Lo primero que debemos hacer es importar los valores de $x$ e $y$ del archivo de texto en Python. Como ya se aprendió anteriormente, los datos se pueden importar a un DataFrame usando la librería pandas (ir a Python: Pandas DataFrame manipulación de datos). Sin embargo, en este caso, importaremos los datos a un array utilizando la librería numpy.

#Importing library
import numpy as np


#Importing text file
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)
print(data)

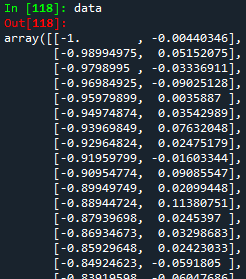
La imagen de arriba muestra una pequeña parte de todos los datos. Como se puede notar, es una matriz 2D donde los valores $x$ e $y$ están delimitados por la coma (derecha e izquierda respectivamente). Para tener una idea de cómo se ven estos datos, primero establezcamos nuestros valores $x$ e $y$ y luego, grafiquémoslos. Para ello, utilizaremos la librería matplotlib.pyplot.

#Importing libraries
import matplotlib.pyplot as plt


#Setting x- and y- values
x = data[:,0]
y = data[:,1]


#Plotting data
plt.plot(x,y,'o')
plt.title('Original data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

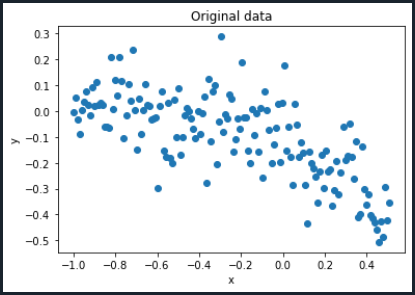
Ahora, llegó el momento de definir la matriz de Vandermonde. En álgebra lineal, una matriz de Vandermonde es una matriz con términos de una progresión geométrica en cada fila:

Observar que d representa el grado del polinomio y n representa el número de valores de $x$. En este caso, dado que tenemos una relación lineal, nuestra matriz de Vandermonde será:

Tener en cuenta que la matriz de Vandermonde tiene dimensiones $nx2$ ($n$ filas y 2 columnas). En Python, lo construiremos de la siguiente manera:

#Vandermonde matrix
v = np.vstack((np.ones(len(x)),x)).T
print(v)

¿Cómo entender el código anterior? Bien, primero se crea el vector-columna de 1s. Recuerda que el número de 1 en esa columna es el mismo que los valores de $x$. Para hacerlo, usamos la función np.ones. Entonces, la segunda columna es exactamente como el x-array ya definido. Finalmente, la función np.vstack se utiliza para unir estos dos arrays en uno solo.

Pero, ¡cuidado! Después de hacer esto, se obtiene una matriz de $2xn$ (2 filas y $n$ columnas). Para que esta matriz tenga una dimensión $nx2$, debemos transponerla. En Python, esto se hace usando la función .T. Si se ejecuta el código anterior, se obtiene la matriz de Vandermonde.

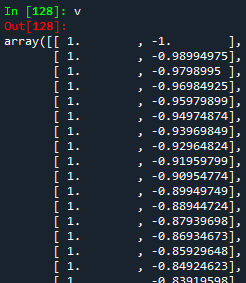
Para verificar las dimensiones del array, usamos la función shape.

#Checking dimensions
dimensions_v = v.shape
print(dimensions_v)

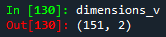
¡Ahora es el momento de encontrar los coeficientes! Como para $x$, expresaremos los coeficientes como una matriz. Para hacerlo, recordemos un poco de álgebra lineal. Dado que el objetivo es minimizar el error cuadrático medio del sistema, la matriz de coeficientes se definirá como:

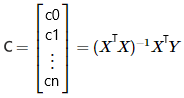
Escribamos la fórmula anterior en Python.

#Defining the coefficient matrix
coeff = np.linalg.inv(v.T.dot(v)).dot(v.T).dot(y)

En Python, la inversa de una matriz se escribe usando la función np.linalg.inv(), y para multiplicar matrices es necesario usar la función .dot (), de lo contrario, si escribe el símbolo común para la multiplicación '*', obtendrá un error. Si imprimimos la variable coeff, obtendremos un array compuesto por todos los coeficientes (en este caso solo $c_0$ y $c_1$)

#Printing the coefficient matrix
print(coeff)

El paso final es construir la relación lineal. Para esto, simplemente escribiremos la fórmula que describe esta relación.

#Setting the linear relationship
y_lineal = v.dot(coeff)
print(y_lineal)

Para saber cómo se ve la línea recta a través de todos los valores de $x$ e $y$ dados inicialmente, hagamos un gráfico.

#Plotting


#Initially given x- and y-points
plt.scatter(x,y)


#Linear regression points
plt.plot(x, y_lineal, color='red')


#Naming the graph, x- and y-axis
plt.title('Matrix multiplication')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

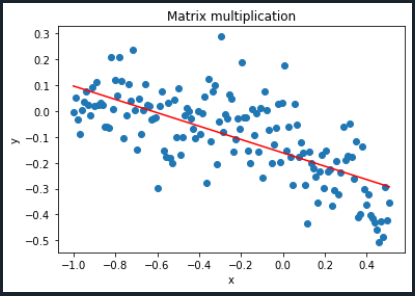
Observar que los puntos azules son los valores $x$ e $y$ dados inicialmente y la línea roja es el modelo de regresión lineal que se acaba de construir.

El código final de Python se verá así:

#Importing libraries
import numpy as np
import matplotlib.pyplot as plt


#Importing text file
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)
print(data)


#Setting x- and y- values
x = data[:,0]
y = data[:,1]


#Plotting data
plt.plot(x,y,'o')
plt.title('Original data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()


#Defining the Vandermonde matrix
v = np.vstack((np.ones(len(x)),x)).T
print(v)


#Checking dimensions
dimensions_v = v.shape
print(dimensions_v)


#Defining the coefficient matrix
coeff = np.linalg.inv(v.T.dot(v)).dot(v.T).dot(y)


#Printing the coefficient matrix
print(coeff)


#Setting the linear relationship
y_lineal = v.dot(coeff)
print(y_lineal)


#Plotting


#Initially given x- and y-points
plt.scatter(x,y)


#Linear regression points
plt.plot(x, y_lineal, color='red')


#Naming the graph, x- and y-axis
plt.title('Matrix multiplication')
plt.xlabel('x')
plt.ylabel('y')


plt.show()

¡Felicitaciones! Ya diste el primer paso hacia el aprendizaje automático. ¡A seguir adelante! En el siguiente tutorial, se explicará un segundo método para hacer regresión lineal. Para descargar el código completo y el archivo de texto con los datos usados en este tutorial, haz click aquí.