¿Cómo podemos aprender un lenguaje de programación? El método más eficiente es la ingeniería invertida, es decir, para aprender un lenguaje vamos a coger un código ya desarrollado y a partir de él vamos a intentar entenderlo para posteriormente modificarlo. En este artículo  usaremos este método para obtener nociones del lenguaje de programación Python. Como punto de partida nos enfocaremos en la importación y el procesamiento de datos, es decir, obtendremos unas gráficas a partir de datos almacenados en archivos de texto. Considero este como el pilar para entender un lenguaje de programación porque fácilmente podrás aplicarlo a tus tareas cotidianas. Por ejemplo, si eres estudiante, en algún momento te pedirán como trabajo obtener algunas gráficas. La mayoría de tus compañeros usará Excel, pero tú, después de leer este artículo, optarás por usar Python, porque sabrás que cuanto más uso le des a un lenguaje de programación, más visión tendrás para crear cosas a futuro.

Antes de empezar este ejercicio, debes tener instalado Jupyter Notebook en tu ordenador. La forma más practica de instalarlo es considerando Anaconda. Hecho esto, debes descargar los archivos de mi repositorio de Github. Mayores detalles aparecen explicados en el siguiente video:

(video aún no disponible)

El repositorio contiene el código de Python import-plot.ipynb que podrás abrir y correr usando, por ejemplo, Jupyter Notebook. También contiene una carpeta con 37 archivos de texto que corresponden a los datos que usaremos para hacer nuestras primeras gráficas. Por ejemplo, el primer archivo de texto viene dado por:

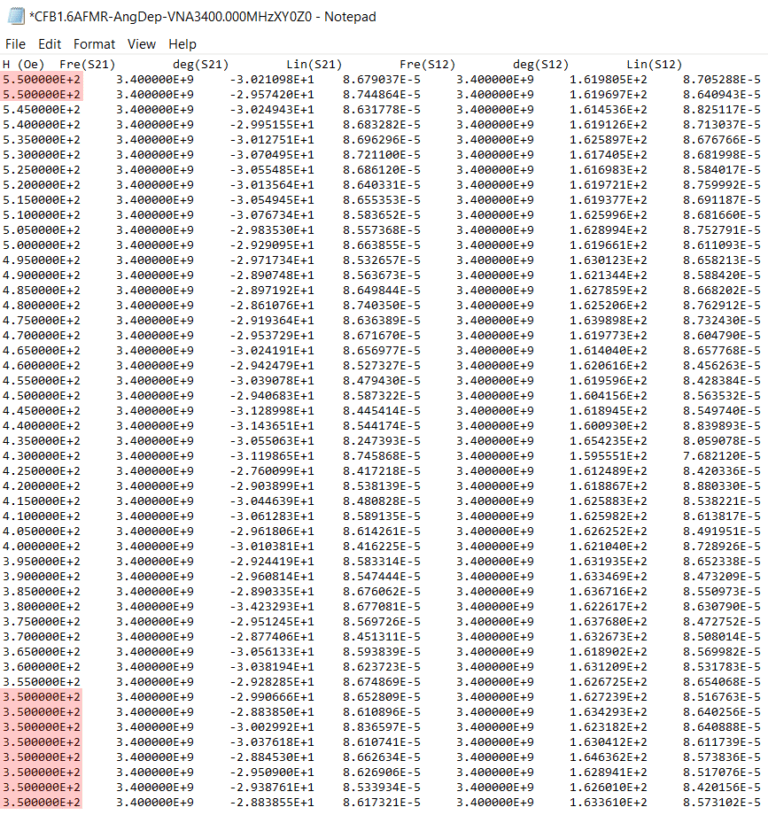
Todos los archivos de texto tienen el mismo formato. En la primera fila están los nombres: H (Oe), Fre(S21), deg(S21), Lin(S21), Fre(S12), deg(S12), Lin(S12), y en las subsiguientes los valores numéricos. Como puedes ver en la Fig. 1, la primera columna tiene datos repetidos, estos aparecen resaltados en color rojo. Como primer paso, lo que vamos a hacer será importar los 37 archivos de texto en Python pero omitiendo los datos repetidos, es decir, al momento de importar cada archivo consideraremos únicamente los datos que van de la línea 2 hasta la línea 42.  Claro está, debes tener presente que en Python se empieza a contar a partir del número cero, i.e.,

Adicionalmente, al momento de leer las líneas, tenemos que leerlas hasta la línea 43 porque Python no considera la línea de cierre. Esto lo entenderás fácilmente accediendo al código, el cual contiene una explicación detallada de la parte técnica. Debes notar que hasta este punto no es tan importante saber de que tratan los datos porque simplemente los estamos importando. Como siguiente paso, queremos que los datos importados se vean de la siguiente forma:

En la Fig. 2 tenemos la transpuesta de los datos importados, es decir, las que fueron columnas (filas) en la Fig. 1 ahora pasan a ser las filas (columnas). Pero no solo eso, el siguiente paso será invertir el orden de las columnas, de esa forma obtendremos lo siguiente:

Como puedes apreciar en la Fig. 3, nuestros datos están ordenados de tal forma que la primera fila empieza en 3.50e+02 y culmina en 5.50e+02.  Ahora procedamos con las gráficas. Por ejemplo, si queremos graficar Fre (S21) vs H (Oe), entonces de la Fig. 3 tendríamos que elegir las dos primeras filas y almacenarlas en pares (x,y), de esa forma tendríamos:

Esta gráfica nos daría una recta horizontal porque Fre (S21) es una constante para todos los valores de H. Ahora pasaré a explicarte de que tratan estos datos, no obstante, ten presente que no es tan importante y solo lo haré para despejar tu curiosidad. Estos datos pertenecen a un experimento de medición. Los resultados fueron publicados en el siguiente enlance: arxiv.org/pdf/2001.05135.pdf. En él, los autores midieron una señal de corriente alterna en un material que estaba sujeto a un campo magnético. Estas mediciones fueron hechas en dos configuraciones denotadas S12 y S21. Una señal de corriente alterna se expresa matemáticamente como:

Teniendo esto presente, la Fig. 1 ahora cobra sentido, se han colectado los valores de la amplitud (Lin), la frecuencia (Fre) y la fase (deg) de la corriente alterna para distintos valores del campo magnético H y para las dos configuraciones dadas (S12 y S21).  Todos estos datos aparecen en cada uno de los archivos, pero ¿por qué existen 37 archivos? Esto se debe a que además de estudiar cómo influye la magnitud del campo magnético en la señal de corriente alterna, también se estudio la influencia de su posición angular, es decir, el campo H fue aplicado  en distintas posiciones angulares, para ser exactos, en 0, 5, 10,..., 175 y 180 grados, dando un total de 37 posiciones angulares, o lo que es, 37 archivos de texto. Resuelta la curiosidad, ahora graficaremos lo siguiente:

En el eje x consideramos el campo magnético H y en el eje y consideramos la amplitud relativa (r) de la señal, la cual está dada respecto a un valor fijo. En este caso el valor fijo será  la amplitud cuando H=355. Recuerda que existen dos configuraciones, S12 y S21, por tanto, tendremos dos tipos de gráficas. Adicionalmente, para cada una de estas gráficas vamos a tener que juntar los datos de los 37 archivos de texto porque queremos que todas las posiciones angulares estén presentes. Se ve un poco engorroso y por eso en Python haremos uso de bucles para alcanzar este objetivo. Te invito a explorar el código para entender mejor de qué te estoy hablando.

Finalmente, para concluir esta experiencia, haremos uso de una gráfica en dos dimensiones. Si  r es la amplitud relativa de la señal, entonces r depende de dos variables, la posición angular y la magnitud del campo H. Esto implica que r puede ser visualizada en un plano 2D:

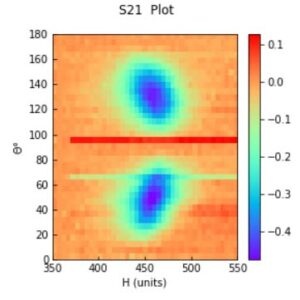
En la Fig. 4 tenemos la gráfica en dos dimensiones para el caso S21, en el eje x tenemos la magnitud del campo magnético H y en el eje y la posición angular; para cada par (x,y), existe un valor definido de r. Como puedes apreciar, las gráficas 2D ofrecen un resultado mucho más interesante...

Te invito a correr el código para capturar la esencia del artículo y con esto... bienvenido al mundo de la programación.