Si no recuerdas qué es un polinomio, ¡no te preocupes! Aquí en ПЕРУ, te refrescamos la memoria.

¿Qué es un polinomio? Es una suma de términos finitos que tiene la siguiente forma: \[y = c_{0}*x^{0} + c_{1}*x^{1} + c_{2}*x^{2} + ... + c_{n}*x^{n }\]

Como se ve, cada término tiene la forma $c_n*x^n$, donde $c_n$ es el coeficiente, $n$ es el grado del polinomio, y $x$ es la variable. ¡Es muy importante mencionar que la variable debe estar elevada a una potencia entera positiva solamente! Sin embargo, ¡los coeficientes pueden ser cualquier número!

Ahora, probablemente te estés preguntando si el grado del polinomio es 1, ¿entonces se sigue llamando polinomio? ¡Eso es correcto! Lo que significa que ya has aprendido Regresión polinomial (La regresión lineal es un caso particular de regresión polinomial donde el polinomio tiene grado 1.

Dicho esto, ¡comencemos! Como recordarás del tutorial anterior, Python tiene una biblioteca llamada scikit-learn (ir a Python Aprendizaje Automático: Regresión Lineal (II)). Primero, importemos los datos. Los datos usados para este tutorial son similares a los usados en el tutorial de Regresión Lineal, pero ahora tienen más puntos para $x$ e $y$

Lo primero que se debe hacer es importar el archivo de texto que contiene los datos (que debe guardarse en la misma carpeta que su Python script), luego definir los valores $x$ e $y$ para luego graficarlos y tener una comprensión gráfica de los datos. Además, el array $x$ se convertirá de 1D a 2D array usando la función reshape(). (Se pueden encontrar más detalles en Python Aprendizaje Automático: Regresión Lineal (II)

#Importing libraries
import numpy as np
import matplotlib.pyplot as plt


#Importing text file
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)
print(data)


#Setting x values
x = data[:,0]
print(x)


#Setting y values
y = data[:,1]
print(y)


#Converting the 1D-array into 2D-array
x_reshape = x.reshape(-1,1)
print(x_reshape)


#Plotting data
plt.plot(x,y,'o')
plt.title('Original data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

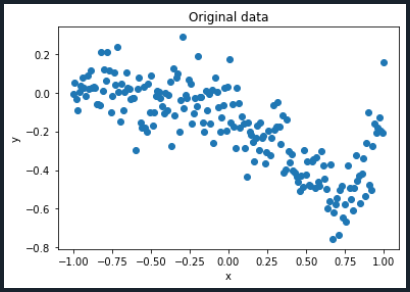
Ahora es el momento de definir el grado del polinomio. Recuerde que cuanto mayor sea el grado, más preciso será el modelo de regresión. Para hacer esto, se necesita la librería Python PolynomialFeatures.

#Importing library
from sklearn.preprocessing import PolynomialFeatures


#Setting the polynomial degree
degree = PolynomialFeatures(degree = 5)

Para ajustar los valores de $x$ al grado polinomial definido, se necesita la función fit().

#Fitting the polynomial to the degree set previously
polynomial = degree.fit(x_reshape)

Ahora, al igual que en la regresión lineal, es necesario construir nuestra matriz de Vandermonde (ir a Python Aprendizaje Automático: Regresión Lineal (I) para más detalles).

#Creating our Vandermonde matrix according to the degree set previously
Vandermonde_matrix = degree.transform(x_reshape)
print(Vandermonde_matrix)

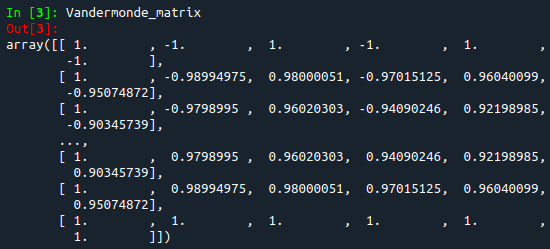
En la figura anterior, la primera columna es $x^0$, la segunda es $x^1$, y así sucesivamente hasta la sexta columna, que es $x^5$ (5 es nuestro grado polinomial definido). El número de filas será igual al número de $x$ puntos importados del archivo de texto.

Ahora es el momento de construir el modelo de regresión polinomial. Para este propósito, se necesita la librería LInearRegression. Si, leíste correctamente. Dado que la regresión lineal es un caso particular de la regresión polinomial, como se explicó anteriormente, se necesita dicha librería.

#Creating the polynomial regression model
model = LinearRegression()

Después de haber construido el modelo, es necesario ajustar los valores $x$ e $y$ al modelo definido. Para este propósito, se necesita la librería fit. Esto significa que el modelo se entrenará obteniendo el valor de $y$ para cada valor de $x$.

#Training the model (Fitting the Vandermonde matrix to the y-values)
train_model = model.fit(Vandermonde_matrix, y)

Ahora que el modelo está debidamente entrenado, ¡es hora de usarlo! Predeciremos los valores de $y$ correspondientes en función de cada valor de $x$. Para ello se necesita la función predict.

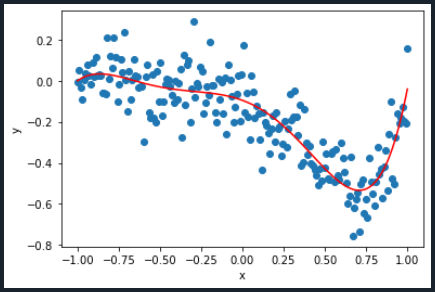
Finalmente, el último paso es graficar. Para tener una mejor comprensión de lo que se acaba de hacer, se graficarán los valores $x$ e $y$ del modelo de regresión polinomial y los valores iniciales $x$ e $y$.

#Plotting the Polynomial Regression model
plt.plot(x,y,'o')
plt.plot(x,y_predicted,color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

El código final de Python tendrá el siguiente aspecto:

#Importing libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures


#Importing text file
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)
print(data)


#Setting x values
x = data[:,0]
print(x)


#Setting y values
y = data[:,1]
print(y)


#Converting the 1D-array into 2D-array
x_reshape = x.reshape(-1,1)
print(x_reshape)


#Plotting data
plt.plot(x,y,'o')
plt.title('Original data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()


#Setting the polynomial degree
degree = PolynomialFeatures(degree = 5)


#Fitting the polynomial to the degree set previously
polynomial = degree.fit(x_reshape)


#Creating our Vandermonde matrix according to the degree set previously
Vandermonde_matrix = degree.transform(x_reshape)
print(Vandermonde_matrix)


#Creating the polynomial regression model
model = LinearRegression()


#Training the model (Fitting the Vandermonde matrix to the y-values)
train_model = model.fit(Vandermonde_matrix, y)


#Getting the predicted y-values according to our x-Vandermonde matrix
y_predicted = train_model.predict(Vandermonde_matrix)


#Plotting the Polynomial Regression model
plt.plot(x,y,'o')
plt.plot(x,y_predicted,color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

¡Felicitaciones! Acabas de aprender los conceptos básicos de las regresiones. ¡Sigue aprendiendo! Para descargar el código completo y el archivo de texto con los datos usados en este tutorial, haz click aquí.