¿Alguna vez te has preguntado si estamos solos en el universo? Aunque suene curioso, un juego tan sencillo como la ruleta nos puede permitir elucidar una respuesta. Por eso, en este artículo, intentaremos vencer a la ruleta explorando sus conceptos matemáticos y lo haremos haciendo uso de un lenguaje de programación. Al final, con todas estas herramientas, responderemos la filosófica pregunta si existe vida en otros mundos. Si nunca has ido a un casino, quizás no sepas de qué te estoy hablando, el juego de la ruleta es muy sencillo, en un tablero existen ciertos números y el objetivo es adivinar cuál es el número ganador. Mayores detalles en el siguiente enlace: ¿Cómo se juega la ruleta?

El lenguaje de escritura que usaremos será Matlab, posiblemente no lo tengas en tu ordenador, pero no te debes preocupar porque su primo más cercano, Octave, es gratuito y lo puedes descargar aquí. Todos los códigos de Matlab funcionan correctamente en Octave, entonces no tendrás problemas si deseas reproducir los resultados que te daré. Un resumen de este artículo aparece en el siguiente video, en él detallo como correr los códigos en Octave. Aquí directamente vamos a discutir los resultados finales (los códigos los podrás descargar de mi repositorio de Github):

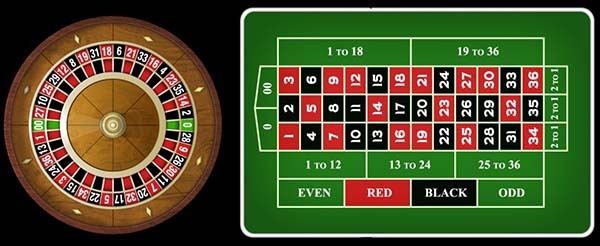
En la Fig. 1 te muestro como luce una ruleta americana, la europea se diferencia por el hecho que en vez de dos ceros, existe solo 1, es decir, en total, la ruleta europea cuenta con 37 números (del 0 al 36) y la americana con 38. En este artículo haremos 3 tipos de apuestas que engloban el total posible de apuestas que existe en este juego de azar. La primera la denominaremos la apuesta determinística, la segunda, la apuesta aleatoria, y la tercera, la apuesta de Martingale. Todas las demás que se te puedan ocurrir, serán una combinación de estas tres.

1. Apuesta determinística

En nuestro primer intento por vencer a la ruleta haremos las siguientes apuestas determinísticas y computaremos cuánto podríamos ganar:

Decimos que es determinístico porque estamos determinando lo que queremos apostar. Estas apuestas aparecen simuladas en el archivo rouletteDeterministic.m. En él consideramos un millón de juegos para cada tipo de apuesta, ¿por qué tantos? Porque el objetivo es ganar a largo plazo y para eso tenemos que asumir que vamos a jugar muchísimas veces, además si fuese solo uno o veinte juegos, la suerte pasaría a convertirse en un factor determinante y aquí nuestro primer objetivo es vencer a la ruleta usando solamente matemáticas. En la Tabla I, la relación x/1 en la columna de pago significa que por cada dólar apostado ganamos x dólares, e.g., 35/1 significa que si ganamos la apuesta, el casino nos devuelve 36 USD, 35 ganados más 1 apostado. Los resultados obtenidos en un millón de juegos son los siguientes:

Como primera conclusión podemos observar en la Tabla II que cualquiera sea la apuesta determinística que hagamos, al cabo de un millón de juegos, siempre terminaremos perdiendo alrededor de 26 000 USD en la ruleta europea y 52 000 USD en la ruleta americana, es decir, si creemos que hoy tuvimos mala suerte y mañana recuperaremos las pérdidas, pues estaremos equivocados porque lo único que conseguiremos con los días será acumular un millón de juegos y así aumentar las pérdidas a los valores dados en la Tabla II, entonces, en una apuesta determinística, no debemos ser incautos ya que cuanto más juguemos necesariamente más perderemos. La segunda conclusión de los resultados dados es que podemos confirmar que la ruleta americana otorga mayores pérdidas, por tanto, nunca debemos elegir este tipo de ruleta porque al hacerlo únicamente estaremos perdiendo más dinero. Como tercera conclusión podemos decir que sin importar el tipo de apuesta determinística que hagamos, las pérdidas serán las mismas. Posiblemente aquí me puedas refutar y decir, por ejemplo, que en la Tabla II podemos ver que para la ruleta europea la apuesta al rojo nos botó -26 410 USD y la apuesta al cero nos botó -28 684 USD, entonces conviene apostar al rojo para perder un poco menos. Pues si tú intentas correr el programa nuevamente posiblemente obtengas que el rojo bota pérdidas mayores. Esto se debe a que a pesar que consideramos un millón de juegos, existe aún ese factor suerte regido por la aleatoriedad que podría inclinar la balanza a una apuesta sobre otra; no obstante, esta inclinación se hace más y más pequeña conforme aumenta el número de juegos, porque cuanto más juguemos, necesariamente las matemáticas pasan a tomar el control. Entonces, ¿cuáles son estos resultados netamente matemáticos? Sin importar si es apuesta al rojo, o al cero, o al grupo del 1 al 12, en la ruleta europea siempre obtendremos 48.6% como porcentaje en ganancias y en la americana 47.3%, y tal como puedes apreciar en la Tabla II, los resultados de un millón de juegos que yo ejecuté son cercanos a estos valores netamente matemáticos. Para entender estos valores porcentuales, enfoquémonos en la ruleta europea y consideremos que jugamos 100 juegos con una apuesta de un dólar por cada juego. En el caso de la apuesta al rojo, el pago es 1/1, esto implica que si ganamos en la mitad de estos juegos, es decir, en el 50% de ellos, entonces la ganancia es nula porque en la mitad lo perdimos todo y en la otra mitad recuperamos esas pérdidas, por tanto, el 50% es sinónimo de no haber ganado ni perdido nada. Por debajo del 50% la ganancia pasará a tomar valores negativos. Este valor porcentual nos servirá de base para derivar los porcentajes netamente matemáticos. En la apuesta al rojo, la probabilidad de ganar en cada juego es 18/37 porque solo existen 18 números de color de rojo de un total de 37. Porcentualmente esto es equivalente al 48.6%. Por tanto, si son 100 juegos, esto implica que ganaremos en 48.6 de ellos, lo cual nos otorgaría, con un dólar de inversión en cada juego, 48.6 x 2 = 97.2 USD. Si la inversión total fue 100 USD, al final estamos obteniendo una ligera pérdida. Asumiendo que el 50% representa una ganancia nula, es decir, ingresos finales de 100 USD, ¿cuál es el porcentaje en ganancias dado por 97.2 USD? Una regla de tres simple nos dice que es 48.6%. En el caso particular de la apuesta al rojo, el porcentaje en ganancias es igual a la probabilidad de ganar en cada juego, y esto se debe a que el pago es 1/1. El análisis es un poco más complejo cuando apostamos al grupo del 1 al 12. En este caso la probabilidad de ganar en cada juego es 12/37, o mejor dicho 32.4%; no obstante, como el pago es 2/1, el porcentaje en ganancias pasa a ser 48.6%. Para entenderlo, si son 100 juegos, matemáticamente, esto implica en 32.4 de ellos ganaremos, entonces el casino nos devolverá 32.4 x 3 = 97.2 USD, lo cual es exactamente igual al caso de la apuesta al rojo. Finalmente, en el caso de la apuesta al cero, es curioso, pero matemáticamente la probabilidad de ganar en cada juego es de apenas 1/37, o mejor dicho 2.7%, no obstante, como el pago es 35/1, el porcentaje monetario vuelve a ser 48.6%, porque el dinero recaudado en 100 juegos viene dado por 2.7 x 36 = 97.2 USD. A todo esto, el objetivo si queremos derrotar a la ruleta debería ser desarrollar un algoritmo capaz de otorgarnos un porcentaje en ganancias por encima al 50%... ¿será posible?

2. Apuesta aleatoria

En la Tabla II nos enfocamos en una apuesta determinística, es decir, determinamos exactamente lo que queríamos apostar. En este segundo intento por derrotar a la ruleta usaremos apuestas aleatorias, ¿existirá alguna diferencia? Para responderlo, consideraremos dos tipos de apuestas en un millón de juegos: i) En cada juego apuesto al mismo número (determinístico). ii) En cada juego apuesto a un número arbitrario (aleatorio). En ambos casos el pago es 35/1 porque estamos apostando a un solo número. Para esto usaremos el archivo rouletteStochastic.m. Los resultados obtenidos son los siguientes:

En la Tabla III observamos, que cualquiera sea el tipo de apuesta, el resultado seguirá siendo el mismo, es decir, no importa si usamos estrategias aleatorias o determinísticas, las variaciones serán mínimas, i.e., muy cerca al  48.6% en la ruleta europea y al  47.3% en la ruleta americana. Esto nos permite inferir que un evento no influye en el siguiente, es decir, cada apuesta es una apuesta independiente. Aunque suene curioso, no porque salieron 10 ceros continuos en el juego, la probabilidad es alta de que en el subsiguiente juego deje de salir. Este es un error común en el que caen los jugadores de la ruleta porque afirman que estadísticamente hablando todos los números deben salir en la misma proporción, entonces si uno ya salió muchas veces pues está destinado a salir mucho menos. Esto es cierto, todos los números están destinados a salir en la misma proporción, pero la estadística no se hace con 20 juegos sino con un millón, recuerda que cuanto más juguemos es cuando las matemáticas empiezan a tomar el control. Ahora pensemos que el jugador es capaz de jugar un millón de veces y resulta que en sus últimos 10 juegos salen puros ceros. Curiosamente, todos los números habrán salido en la misma proporción, entonces que el cero salga 10 veces más que todos los demás no tendrá ninguna relevancia ya que es una ínfima diferencia comparada al millón. Por ende, si bien la estadística nos brinda cierta información, de nada sirve porque no podemos aplicarla para ganar.

3. Apuesta de Martingale

En las dos primeras apuestas hemos fallado en vencer a la ruleta, en este tercer intento, usaremos la estrategia más famosa que existe: Martingale. Para correr el algoritmo, usaremos el archivo rouletteMartingale.m. En palabras sencillas, esta estrategia consiste en doblar la apuesta en caso pierdas y reiniciar el juego en caso ganes. A modo de ejemplo, aquí apostaremos al color rojo considerando una ruleta europea. Nuestra primera apuesta será de 1 USD. Si perdemos, la siguiente será de 2 USD, si continuamos perdiendo, la siguiente será de 4, y así sucesivamente en potencias de 2^j , donde j empieza en cero y va aumentando progresivamente hasta ganar. Al ganar, volvemos a jugar desde j=0. De esta forma nunca perderíamos, porque al doblar la apuesta estaríamos recuperando el valor perdido, ¿verdad? Los resultados en un millón de juegos aparecen a continuación:

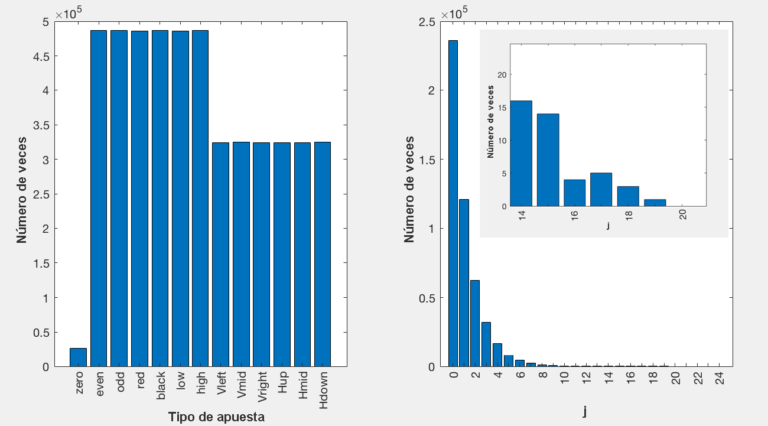
En la Fig. 2(izq.) estamos graficando cuántas veces han salido cada tipo de apuesta, mayores detalles aparecen en el archivo rouletteMartingale.m. Como puedes observar, se cumple lo dicho en la sección anterior, que en un millón de juegos todos los números deben salir en la misma proporción, es decir, saldrán prácticamente la misma cantidad de rojos y negros (red & black), pares e impares (even & odd), altos y bajos (low & high), etc. En la Fig. 2(der.) estamos graficando la apuesta de Martingale. Como puedes apreciar, en un millón de juegos es factible obtener, al menos una vez, j=19, es decir, puede darse el caso que el color rojo no salga en 19 juegos consecutivos, algo que parece ilógico de creer, pero que estadísticamente es un fenómeno real. Ten presente que este resultado es para un millón de juegos que yo ejecuté, posiblemente si tú ejecutas el programa, obtengas un j aún mayor, porque ciertamente la probabilidad de obtener  j más allá de 19 nunca será cero. En términos generales tenemos:

P es la probabilidad de obtener el rojo en el n-ésimo intento, donde j = n-1. e.g., ¿cuál es la probabilidad de que en el primer intento salga el rojo (j=0)? 18/37, y ¿cuál es la probabilidad de que recién en el tercer intento salga el rojo (j=2)? (19/37)² (18/37). El primer factor refleja la probabilidad de no obtener el rojo en j intentos porque son 19 números de un total de 37 que no son rojos y el segundo factor refleja la probabilidad de si obtenerlo porque existen 18 rojos de un total de 37. Como puedes apreciar, por más que j sea muy grande, la probabilidad nunca será cero, solamente será mucho más pequeña. Y en un millón de juegos, ¿cuántas veces podría darse el caso de no obtener el rojo en j intentos? A modo de ejemplo, para j=19 tendríamos 1 000 000 * (19/37)¹⁹ (18/37)=1.54. Por eso, es factible que cada vez que computemos un millón de juegos, nos salga para j=19 el valor de 1, pero ¿qué pasa si consideramos un trillón de juegos? Las matemáticas nos dicen que el evento j=61 es factible que ocurra al menos una vez, es decir, es posible que 61 veces consecutivas no salga el rojo. Inverosímil pero posible. Ahora, esto no debe causarnos confusión, el hecho que más juegos nos revelen "j_s" más grandes no significa que nunca saldrán si solo jugamos 100 o 1 000 veces, al contrario, quizás para mala suerte nuestra, en toda la historia de la ruleta, justo nuestro juego sea aquel con j=61, claro que esa probabilidad es tan baja que si se llega a dar, efectivamente seríamos los seres con menos suerte en el planeta, o quizás en el universo, porque como puedes apreciar en la Fig. 2(der.), a medida que j aumenta, la cantidad de veces que esto llega a ocurrir es cada vez menor y va cayendo en la proporción (19/37)^j, pero ¿será acaso Martingale suficiente para vencer a la ruleta? Pues no, ya que si solo asumimos un millón de juegos, debemos estar preparados, por ejemplo, para un evento con j=19, es decir, tener la capacidad de apostar 2²⁰ - 1 = 1 048 575 USD, porque no existe razón alguna para creer que nunca tendremos la mala suerte que esta racha negativa sin el rojo llegue a ocurrir en nuestros primeros juegos. Adicionalmente, la estrategia de Martingale no otorga grandes ganancias, porque si estamos doblando la apuesta es porque estamos perdiendo en los juegos previos y acumulando valores negativos, al final, apostando 1 048 575 USD lo único que conseguiremos será recuperar todo el dinero perdido, es decir, las ganancias son mínimas y las pérdidas pueden ser gigantescas porque si nos quedamos sin dinero ya no podremos doblar la apuesta y recuerda que j=19 no es el límite, en realidad no existe límite y debemos ser conscientes que para estar seguros de ganar nuestras reservas monetarias deben ser infinitas. Pero aquí no termina la historia porque los casinos, para que perdamos el dinero rápidamente, pondrán un límite a la apuesta, es decir, dirán que máximo podremos apostar al rojo un máximo de 200 USD, esto a la larga, como ves en la Fig. 2(der.), es muy perjudicial, porque existen muchos juegos por encima de j = 8 que no podremos recuperar porque tenemos una apuesta restringida a un máximo de 200 USD. Entonces si bien Martingale es una estrategia muy popular, matemáticamente hablando es de las peores que existen y jamás debemos usarla.

Para culminar el análisis, veamos qué ocurre si solo consideramos 20 juegos, los resultados aparecen a continuación:

Curiosamente, en 20 juegos es factible diferenciar que salgan más de un tipo que del otro, esto lo puedes notar comparando la Fig 2(izq.) con la Fig. 3(izq.), en esta última claramente distinguimos que han salido más rojas que negras, lo cual nos permite intuir que si fuésemos capaces de predecir cuál es el color favorito en 20 juegos consecutivos, pues ganaríamos constantemente. ¿Cuál es el inconveniente? Que no lo podemos saber, porque esto está sujeto a la suerte, y tal como dije en un inicio, si son pocos juegos es más suerte que matemáticas porque la estadística no funciona en cantidades muy pequeñas. De todas formas obtenemos una conclusión muy importante para vencer a la ruleta: "Las apuestas determinísticas, aleatorias o de Martingale solo generan pérdidas a largo plazo, por tanto, para vencer, nos conviene hacer uso de la suerte mas que hacer uso de las matemáticas y esto lo podremos conseguir solamente en el corto plazo". Esto implica que si un día vamos al casino y ganamos, por ejemplo, usando la técnica de Martingale en 20 juegos consecutivos, pues jamás debemos volver, porque solamente teniendo pocos juegos en nuestro historial existirá la gran esperanza de vencer, y obviamente si perdemos pues mejor ya no volvamos porque perderemos mucho más.

4. ¿Estamos solos en el universo?

Para responder esta pregunta filosófica vamos a formular un modelo matemático que se basará en el juego de la ruleta y en la apuesta de Martingale. Como recordarás, j representa la cantidad de intentos fallidos, i.e., j = 3 quiere decir que en los tres primeros juegos fallamos en ganar y en el cuarto acertamos. De la misma forma asumiremos que somos los arquitectos del universo y vamos a intentar crear planetas, es decir, cada juego estará asociado a los intentos de creación de un planeta. En caso fallemos, nos veremos forzados a doblar la apuesta. A diferencia del juego de la ruleta, en el juego del universo, doblar la apuesta estará asociado a incorporar un elemento químico adicional y para efectos prácticos diremos que para que exista la vida basta obtener un planeta con  91 elementos químicos, es decir, obtener un set de juegos con j=90. Ten presente que este es un modelo sencillo y no tiene nada de científico ni mucho menos será exacto, pero nos ayudará a vislumbrar si estamos solos en el universo. Consideremos un millón de juegos, es decir, un millón de veces intentaremos crear planetas. En la Fig. 2(der.) ya tenemos la respuesta. Es muy fácil crear planetas con j=0, es decir, en nuestro primer intento usando un único elemento lo conseguimos con facilidad, no obstante, cuando fallamos fuimos agregando  más elementos, al punto que en un millón de intentos obtuvimos un planeta con j=19. ¿Qué necesitamos para llegar a j=90 y así obtener un planeta tan difícil de imaginar a como no obtener las rojas en 90 juegos consecutivos? Pues simplemente necesitamos intentar crear muchos más planetas. ¿Cuántos más? 10¹⁸ nos acercó a j=61. Con unos cálculos matemáticos obtenemos que considerando 10³⁰ intentos de creación es probable conseguir 4 332 casos con j=90, es decir, 4 332 planetas con 91 elementos químicos. Esto nos permite vislumbrar una conclusión muy interesante, que si bien la probabilidad de que un planeta albergue vida es tan pero tan inverosímil como no obtener las rojas en 90 juegos consecutivos, aún así no es cero y basta jugar el juego un número astronómico de veces para que no solo obtengamos 1 planeta con vida, sino quizás, 4 332 planetas, o lo que es mucho más interesante, quizás algunos vengan dados con j=100 o j=150, es decir, creaciones más allá de nuestra simple compresión. Pero lo más curioso es que el universo está expandiéndose y al mismo tiempo nuevos planetas están formándose, es decir, este juego universal se está jugando constantemente y por ende la probabilidad de obtener ese j=90, si bien es ridículamente inverosímil para nuestra comprensión, a escalas astronómicas crecientes es factible y nos permite vislumbrar que indudablemente es mucho más probable que no estemos solos. Esto también nos puede hacer pensar que el arquitecto que creo el universo, no solo es un formidable matemático, sino que al tener control total del tiempo, puede usar la técnica de Martingale a su favor, porque él, a diferencia de nosotros, podrá jugar el juego infinitas veces y no fallar con la creación porque sus "reservas monetarias" no tienen un límite. Te invito a que formules un modelo matemático más complejo haciendo uso de números astronómicos reales, porque este de acá solo fue un ejemplo sencillo para capturar el mensaje final: "Es mucho más probable que no estemos solos y el hecho que existan muchos planetas que no albergan la vida, es parte del proceso regido por la probabilidad para alcanzar algunos cuantos que si la tengan".