En el tutorial anterior, se aprendió cómo construir una regresión lineal usando la multiplicación de matrices (ir a Python Aprendizaje Automático: Regresión Lineal (I)). Ahora, en este tutorial, se usará una biblioteca de Machine Learning Python llamada scikit-learn para este propósito.

Una vez que hayamos importado los datos del archivo de texto, establezcamos nuestros valores $x$ y $y$.

#Importing library
import numpy as np


#Importing text file
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)
print(data)


#Setting x values
x = data[:,0]
print(x)


#Setting y values
y = data[:,1]
print(y)

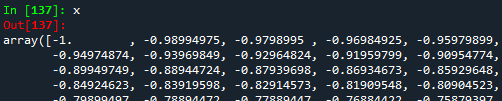
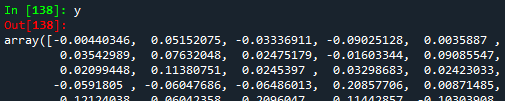
De la figura anterior (un extracto de todos los datos), se puede notar que $x$ y $y$ son arrays 1D. Si queremos trabajar con la librería Python scikit-learn Machine Learning, es necesario convertir los arrays 1D a 2D. Para esto, la función reshape(-1,1).

#Reshaping the array into a vector-column
x2 = data[:,0].reshape(-1,1)
print(x2)


#Reshaping the array into a vector-column
y2 = data[:,1].reshape(-1,1)
print(y2)

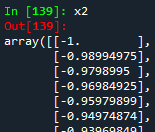
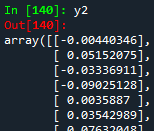
Ahora, podemos construir nuestro modelo de regresión lineal usando el módulo LinearRegression de la librería scikit-learn. No olvide importar dicha librería.

#Importing library
from sklearn.linear_model import LinearRegression


#Building the linear regression model
linear_regression = LinearRegression()
linear_model = linear_regression.fit(x2,y2)

Como se explicó en el tutorial anterior, la relación lineal puede ser \[y = c_{0} + c_{1}*x\], donde $c_0$ es la intersección con el eje $y$, y $c_1$ es la pendiente de la línea. Estos dos coeficientes se pueden encontrar más fácil y rápido gracias a la función LinearRegression().fit(). Para obtener ambos coeficientes se necesitan las funciones intercept_ y coef_.

#Getting the intercept with y-axis
intercept_yaxis = linear_model.intercept_
print(intercept_yaxis)


#Getting the coefficient
slope = linear_model.coef_
print(slope)

En contraste con el enfoque de multiplicación de matrices donde la matriz de coeficientes es un array de dos elementos, ambos elementos ahora se obtienen en dos arrays diferentes de un elemento cada uno. Si se comparan ambos enfoques, tanto la intersección como la pendiente deben ser exactamente iguales. La matriz de coeficientes del tutorial anterior era la siguiente:

Como se ve en ambas imágenes, notamos que ambos coeficientes (intersección y pendiente) son exactamente iguales. ¡Esto significa que hicimos un gran trabajo al hacer la regresión lineal! Finalmente, establezcamos la relación lineal y grafiquémosla.

#Importing library
import matplotlib.pyplot as plt


#Establishing the linear relationship
y_lineal2 = slope*x2 + intercept_yaxis
print(y_lineal2)


#Plotting


#Initially given x- and y-points
plt.scatter(x,y)


#Linear regression points
plt.plot(x2, y_lineal2, color='red')


#Naming the graph, x- and y-axis
plt.title('scikit-learn library')
plt.xlabel('x')
plt.ylabel('y')


plt.show()

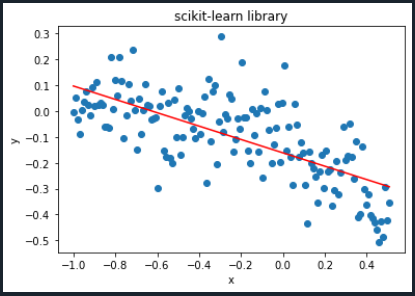
La gráfica que se obtuvo en el tutorial anterior fue la siguiente:

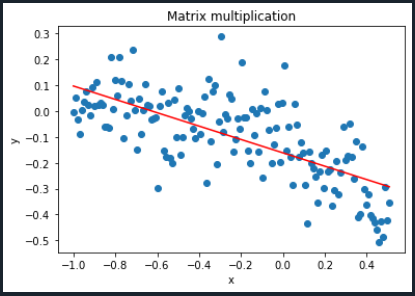
Como se ve en ambos gráficos, ¡podemos decir que son exactamente iguales! El código final de Python tendrá el siguiente aspecto:

#Importing libraries
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt


#Importing text file
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)
print(data)


#Setting x values
x = data[:,0]
print(x)


#Setting y values
y = data[:,1]
print(y)


#Reshaping the array into a vector-column
x2 = data[:,0].reshape(-1,1)
print(x2)


#Reshaping the array into a vector-column
y2 = data[:,1].reshape(-1,1)
print(y2)


#Building the linear regression model
linear_regression = LinearRegression()
linear_model = linear_regression.fit(x2,y2)


#Getting the intercept with y-axis
intercept_yaxis = linear_model.intercept_
print(intercept_yaxis)


#Getting the coefficient
slope = linear_model.coef_
print(slope)


#Establishing the linear relationship
y_lineal2 = slope*x2 + intercept_yaxis
print(y_lineal2)


#Plotting


#Initially given x- and y-points
plt.scatter(x,y)


#Linear regression points
plt.plot(x2, y_lineal2, color='red')


#Naming the graph, x- and y-axis
plt.title('scikit-learn library')
plt.xlabel('x')
plt.ylabel('y')


plt.show()

¡Felicitaciones! Acaba de realizar su primera regresión de aprendizaje automático. En el próximo tutorial, se explicará la regresión polinomial. Para descargar el código completo y el archivo de texto con los datos usados en este tutorial, haz click aquí.