Have you ever wondered if we are alone in the universe? Although it may sound unrelated, a game as simple as roulette can allow us to elucidate an answer. Therefore, in this article, we will try to beat the roulette while exploring its mathematical concepts and we will do so using a programming language. In the end, with all these tools, we will answer the philosophical question: “Are we alone in the universe…?” If you have never been at a casino, you may not know what I’m talking about. Roulette is a very simple game, there are certain numbers on a board and the objective is to guess which one will be the winning number. More details in the following link: How to play roulette

The scripting language that we will use is Matlab, you may not have it on your computer, but you should not worry about it because its closest cousin, Octave, is free and you can download it here. All Matlab codes work in Octave, so you will have no problem reproducing the results given in this article. Details about how to run the codes in Octave are given in the following video. Here we directly discuss the final results (the codes can be downloaded from my repository @Github):

In Fig. 1, I show you what an American roulette looks like, the European one differs by the fact that instead of two zeros, there is only 1, that is, in total, the European roulette has 37 numbers (from 0 to 36) and the American roulette has 38. In this article we will make 3 types of bets that cover the total possible bets that exist in this game. The first bet will be called the deterministic bet, the second one, the random bet, and the third one, the Martingale bet. All other types of bet that you can think of are just a combination of these three.

1. Deterministic bet

In our first attempt to beat roulette we will make the following deterministic bets and compute how much we could win:

We say it is deterministic because we are determining what we want to bet on. These bets are simulated in the code rouletteDeterministic.m, where we consider a million games for each type of bet. Why do we consider a million games? Because the objective is to win in the long term, otherwise, if we only choose to play, for example, twenty games, luck would become an important factor and here our main goal is to beat roulette using just math. In Table I, the x/1 ratio in the payout column means that for every dollar that we bet, we win x dollars, e.g., 35/1 means that if we win the bet, the casino gives us back 36 USD, 35 dollars won plus the dollar of our initial bet. The results obtained in a million games are as follows:

As seen in Table II, our first conclusion is that whatever deterministic bet we make, after a million games, we will always end up losing around 26K USD in the European roulette and 52K USD in the American roulette, that is, if today we had bad luck and we believe that tomorrow we will recover the losses, then we are wrong because the only thing that we will achieve over the days will be to accumulate a million games and thus increase the losses to the values given in Table II, then, in a deterministic bet, we must not be unwary because the more we play, then the more we lose. The second conclusion from the results given in Table II is that we can confirm that the American roulette grants bigger losses than the European roulette, therefore, we should never choose the former one because by doing so we will only be losing more money. As a third conclusion we can say that regardless of the type of deterministic bet we make, the losses will be the same. Possibly here you can refute me and say, for example, that in Table II we clearly see that for the European roulette, betting on red gave us a loss of -26,410 USD, while betting on zero gave us a loss of -28,684 USD, so it is convenient to bet on red to lose a little less. Well, if you try to run the program again, you may get a bigger loss betting on red. This is due to the fact that although we consider a million games, there is still this luck factor governed by randomness that could tip the balance to one bet over the other; however, this inclination becomes smaller and smaller as the number of games increases, because mathematics takes over as we play more. So what are these purely mathematical results? Regardless of whether it is a bet on red, or on zero, or on the group from 1 to 12, in the European roulette we will always obtain 48.6% as a profit percentage and in the American roulette, 47.3%, and as you can see in Table II, the results of a million games that I played are close to these purely mathematical results. To understand these percentage values, let’s focus on the European roulette and let’s consider that we play 100 games betting 1 dollar in each game. In the case of the bet on red, the payout is 1/1, this implies that if we win in half of the games, that is, in 50% of them, then the profit is zero because in half of them we lost everything and in the other half we recover those losses, therefore, 50% represents a zero percentage gain. Below 50% the profit will take negative values. This percentage will serve as basis to derive the purely mathematical results. When betting on red, the winning probability in each game is 18/37 because there are only 18 numbers colored red out of a total of 37. In percentage terms, this is equivalent to 48.6%. Therefore, if we play 100 games, this implies that we will win in 48.6 of them, which would give us, betting one dollar in each game, 48.6 x 2 = 97.2 USD. If the total investment was 100 USD, then in the end we are losing -2.8 USD. Assuming that 50% represents a zero profit level, that is, a return of 100 USD net, what is the profit percentage given by 97.2 USD? A simple rule of three tells us that it is 48.6%. In the particular case of betting on red, the winning probability is equal to the profit percentage, and this is because the payout is 1/1. The analysis is a bit more complex when we bet on the group from 1 to 12. In this case the winning probability in each game is 12/37, or rather 32.4%; however, since the payout is 2/1, the profit percentage becomes 48.6%. To understand this, for 100 games, this implies that in 32.4 of them we will win, then the casino will give us back 32.4 x 3 = 97.2 USD, which is exactly the same result as the one given for betting on red. Finally, when we bet on zero, mathematically, the winning probability in each game is barely 1/37, or rather 2.7%, however, since the payout is 35/1, the profit percentage is again 48.6%, because the casino will give us back, after 100 games, 2.7 x 36 = 97.2 USD. In the end, as you can notice, the objective, if we want to beat roulette, should be to develop an algorithm capable of granting us a profit percentage above 50%… Would it be possible?

2. Random bet

In our second attempt to beat roulette, we will use random bets. Will there be any difference? To answer this, we will consider two types of bets: i) In each game we bet on the same number (deterministic). ii) In each game we bet on an arbitrary number (random). In both cases the payout is 35/1 because we are betting on a single number. To get the results of a million games, we consider the file rouletteStochastic.m. The results obtained are as follows:

In Table III we see that whatever the type of bet we choose, the result will remain the same, that is, it does not matter if we use random or deterministic strategies, the variations will be minimal, i.e., very close to 48.6% in the European roulette and to 47.3% in the American roulette. This allows us to infer that one event does not influence in the next one, that is, each bet is an independent bet. Although it sounds bizarre, not because we got 10 consecutive zeros in our last 10 games, the probability is high that in the subsequent game it will stop coming out. This is a common mistake of roulette players because they claim that statistically speaking all numbers must come out in the same proportion, so if one has already come out many times then it is meant to come out much less in future games. This is actually true, all numbers are meant to come out in the same proportion, however statistics is not done with 20 games but with at least a million games, remember that mathematics begins to take control as long as we play more. Now let’s think that the player is capable of playing a million times and it turns out that in his last 10 games, he gets 10 consecutive zeros. Curiously, by then all numbers would have come out in the same proportion, so getting 10 consecutive zeros at the end will not have any impact since it is a tiny number compared to one million. Therefore, although statistics provide us with certain information, it is useless because we cannot apply it to win.

3. Martingale bet

In the first two attempts we have failed to beat roulette, in this third attempt, we will use the most famous strategy that exists: Martingale. The algorithm is encoded in rouletteMartingale.m. In simple words, this strategy consists of doubling the bet in case you lose and restarting the game in case you win. As an example, here we will bet on red considering the European roulette. Our first bet will be 1 USD. If we lose, the next one will be 2 USD, if we continue to lose, the next one will be 4, and so on in powers of 2^j, where j starts at zero and increases progressively until we win. When we win, we play again from j = 0. In this way we would never lose, because by doubling the bet we would be recovering the money lost, right? The results in a million games are listed below:

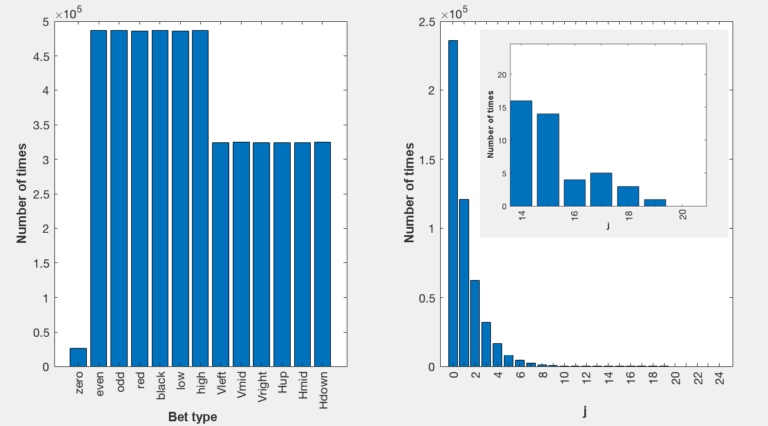
In Fig. 2 (left) we show a histogram of how many times each type of number has come out, more details appear in rouletteMartingale.m. As you can see, what we said in the previous section is true, that in a million games all numbers must come out in the same proportion, that is, we have practically the same amount of reds and blacks, of evens and odds, of highs and lows, etc. In Fig. 2 (right) we are showing the Martingale bet. As you can see, in a million games it is feasible to obtain, at least once, j = 19, that is, it is feasible that the color red does not appear in 19 consecutive games, something that seems illogical, but statistically speaking it is a real phenomenon. Keep in mind that this result is for a million games that I played, possibly if you run the program, you may get a higher j, because certainly the probability of getting j beyond 19 will never be zero. In general we have:

P is the probability of getting red on the nth try, where j = n-1. e.g., what is the probability of getting red on our first try (j = 0)? 18/37, and what is the probability of getting red on the third attempt (j = 2)? (19/37)² (18/37). As you can see, j represents the number of failed attempts because the first factor reflects the probability of not obtaining red in j attempts (there are 19 numbers out of a total of 37 that are not red), and the second factor reflects the probability of obtaining it (there are 18 reds out of a total of 37). Therefore, no matter how large j is, the probability will never be zero, it will only be much smaller. And in a million games, how many times could it be the case that you don’t get red in j tries? As an example, for j = 19 we would have 1,000,000 * (19/37)¹⁹ (18/37)=1.54. Thus, it is feasible that every time we compute a million games, we get once the case j = 19, but what happens if we consider 10¹⁸ games? Mathematics tells us that the event j = 61 is likely to occur at least once, that is, it is possible that 61 consecutive times, red won’t come out. Unbelievable but possible. Now, this should not cause any confusion, the fact that more games reveal bigger “j_s” does not mean that they will never come out if we only play 100 or 1,000 times, on the contrary, perhaps to our bad luck, in the entire history of roulette, our game becomes the one with j = 61, of course the probability is so low that if it happens, we would indeed be the least lucky beings on the planet, or perhaps in the universe, because as you can see in Fig. 2 (right), as j increases, the number of times that this event happens is less and less probable since it falls in the proportion (19/37)^j. But Martingale would be enough to beat roulette? No, because if we only assume a million games, we must be prepared, for example, for an event with j = 19, that is, we must be capable of betting 2²⁰ - 1 = 1,048,575 USD, because there is no reason to believe that this event won’t happen in our first games. Additionally, the Martingale strategy does not provide large profits, because if we are doubling the bet it is because we are losing in the previous games, and therefore by betting 1,048,575 USD, the only thing we will achieve is to recover the money lost, that is, the gains are minimal and the losses can be gigantic because if we run out of money we will no longer be able to double the bet, and remember that j = 19 is not the limit, in fact, there is no limit and we must be aware that to be sure of winning, our money reserve must be infinite. But the story does not end here because the casinos, in order for us to lose more quickly, will put a limit on the bet, that is, they will say that the maximum bet on red is 200 USD, this in the long run, as you can see in Fig. 2 (right), is very harmful, because there are many games above j = 8 that we will not be able to recover because we have a restricted bet to a maximum of 200 USD. So although Martingale is a very popular strategy, mathematically speaking it is one of the worst that exists and we should never use it.

To finish the analysis, let’s see what happens if we only consider 20 games, the results appear below:

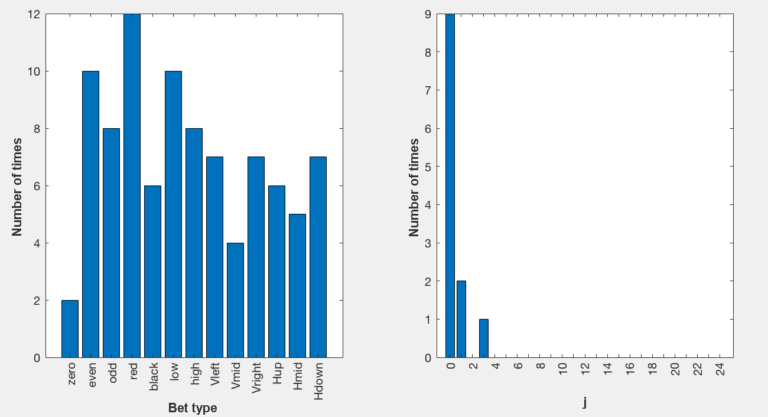
Curiously, in 20 games it is easy to check that we get more numbers of one type than of the other. If we compare Fig. 2 (left) with Fig. 3 (left), we clearly distinguish in the latter that we have gotten more reds than blacks, which allows us to think that if we were able to predict which is the favorite color in 20 consecutive games, then we would constantly win. What is the downside? That we cannot know, because this is subject to luck, and as we said at the beginning, if there are few games it is more luck than mathematics because statistics do not work in small quantities. In any case, we obtain a very important conclusion to beat roulette: "Deterministic, random or Martingale bets only generate long-term losses, therefore, to win, we should use luck rather than mathematics, and we can only achieve this in the short term." This implies that if one day we go to the casino and win, for example, using the Martingale technique in 20 consecutive games, we must never come back, because only if we have a few games in our history we will have great chances of beating roulette, and of course, if we lose, is also better not to come back because we will lose much more in the long run.

4. Are we alone in the universe?

To answer this philosophical question we are going to formulate a mathematical model that resembles the roulette and the Martingale bet. Recalling, j represents the number of failed attempts, i.e., j = 3 means that in the first three games we failed to win and in the fourth we were correct. In the same way, we will assume that we are the architects of the universe and we will try to create planets, that is, each game will be associated with an attempt of creation. In case we fail, we will be forced to double our bet. Unlike the game of roulette, in the game of the universe, doubling the bet will be associated with incorporating an additional chemical element and for practical purposes we will say that for life to exist it is enough to obtain a planet with 91 chemical elements, that is, we need a set of games with j = 90. Keep in mind that this is a simple model and it is not at all scientific, so it is not exact, but it will help us to elucidate if we are alone in the universe. Let’s consider a million games, that is, a million times we will try to create planets. In Fig. 2 (right) we already have the answer. It is very easy to create planets with j = 0, that is, in our first attempt using a single chemical element; however, when we fail, we add more elements, to the point that in a million attempts we obtain a planet with j = 19. What do we need to get a planet with j = 90, a difficult planet, similar to not getting red in 90 consecutive games? Well we simply need to create more planets. How many more? 10¹⁸ brought us closer to j = 61. With some mathematical calculations we obtain that considering 10³⁰ creation attempts it is likely to get 4,332 cases with j = 90, that is, 4,332 planets with 91 chemical elements. This allows us to glimpse a very interesting conclusion, that although the probability of having a planet harboring life is as unlikely as not getting reds in 90 consecutive games, it is still not zero and it is enough to play the game an astronomical number of times, so that we not only get 1 planet harboring life, but perhaps 4,332 planets, or what is much more interesting, perhaps some of them are given with j = 100 or j = 150, that is, creations beyond our simple understanding. But the most curious thing is that the universe is expanding and at the same time new planets are constantly forming, that is, this universal game is constantly being played and therefore the probability of obtaining a planet with j = 90, although it is ridiculously implausible for our understanding, at astronomical scales it is feasible and allows us to glimpse that it is undoubtedly much more likely that we are not alone in the universe. This can also make us think that the architect who created the universe is not only a formidable mathematician but also a very smart gambler, because by controlling time, he can use the Martingale technique to his advantage, because he, unlike us, will be able to play the game infinite times and won’t fail with the creation because his “money reserves” do not have a limit. I invite you to formulate a more complex mathematical model using real astronomical numbers, because the one given here was only a simple example to capture the final message: "It is much more likely that we are not alone in the universe and the fact that there are many planets that do not hold life is part of the process governed by probability to reach a few that do."