A decentralized world

A summary of this section with some extra info appears in the following video:

The most beautiful dreams arise in our childhood when we imagine a new world without wars, without diseases, without borders and social classes. We don't question ourselves how difficult this could be, we just give free rein to our imagination and think that it is possible. It was a 12-year-old boy who thought about bitcoins, he was completely unaware of the financial world but he felt that something was wrong, and to fix it, without knowing how, he realized that he needed to create a currency.

Over the years he developed the tools that would allow him to achieve his goal. And not only that, he also understood how the world economy works. How banks sell the idea of ​​taking care of your money, but instead they use it without telling you. It worked really well because if someone tried to access another account, the bank would block him. To achieve this, in the beginning the bank counted the money by hand, verified the signatures and protected its vaults. Over time, computers made it easier because people began to use credit cards and start making transfers online, that is, money stopped being physical and became a virtual currency. Today most payments or transfers only involve changing data in virtual accounts, so what is money if you no longer have it with you? It is just data! That's all! And in the future it will be completely like that. Banks will have full control of the data and therefore they will do whatever they want. For example, you think that you have 100 USD in your savings account, but the bank has actually borrowed that money without telling you, that is, they are making profits with the money that is supposed to be yours, and on top of that they charge you a fee for "taking care" of your money, so, what can we expect in a future where money becomes a number in a virtual machine? Satoshi understood that it was not good to give so much power to banks, but how could he avoid it...? Decentralizing the data! That was the solution!

To achieve this, he thought of creating a public account. In simple terms this can be regarded as a sheet of paper on which all users will write down the transactions they make. In the digital world, this could be regarded as a text document that is updated by sending it by email. It looks quite easy to implement but a document sent by email is not an efficient method. Satoshi thought of something else, something that he had been using and likely you have used as well. I'm referring to peer-to-peer (P2P) applications such as Ares, Emule, BitTorrent, Limewire, Deluge, etc. These applications allow you to share information without intermediaries, that is, without central entities that have control of the data. In case these names are not familiar to you, I invite you to read the article: "How to download programs using peer-to-peer applications." In this article, considering Deluge, we briefly discuss what peer-to-peer aplications are. In the case of an email service, there are intermediaries, for Gmail it would be Google, for Outlook it would be Microsoft, and as intermediaries they have absolute control of your information, they just behave like banks, but banks of information. In the case of P2P applications this is not the case, the transfer is directly from one PC to another PC. For example, if you would like to download a song, you would do it directly from someone's computer, and then someone else could download it from you because you would already have it on your PC. For this reason, if a new monetary system is meant to exist, it should not be a centralized system, it has to be part of a P2P network, and not only that, it has to be managed with its own currency because the banks would not accept losing the source of their power.

In Fig. 3 I show you the differences of using a bank and of using a public account. At first glance they look exactly the same, but don't be fooled. In the case of the bank (left), dollars are used and the transfers made by Alice, Bob and Tom are entirely controlled by the bank, while in the case of a public account (right), bitcoins (BTC) are used and everyone has the control, that is, everyone has access to the data, but this is where the problem begins, can we trust other people when we have a public account?

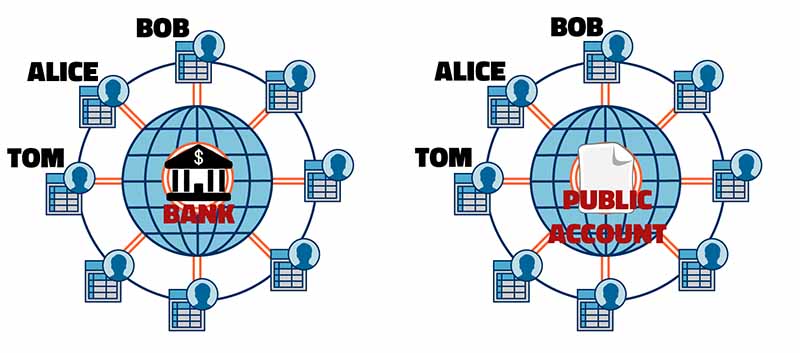
If everyone has access to the public account, then anyone can alter the information. Human beings, by nature, are imperfect, they are subjected to temptations that make them seek their personal interests, therefore, we cannot trust them. For example, Bob can easily have only 10 BTC in his possession but in the public account he could easily write that he transfers 200 BTC to Tom. There is no one who can verify it. Remember that we are in the digital world, and therefore we don't have money to touch, these numbers are just data on a public digital document. How can we make sure that Bob won't make such a move? Satoshi gave a solution: "Let's create a finite number of coins." With this, if Bob tries to transfer more coins than he has, it will be enough to recount the total number of coins and if they do not add up to the universal constant, the transaction will be rejected. Perfect, right? Not really! Now Bob will try a different approach, he will write down on the public account that Tom sends him 5 BTC. If Tom has more than 5 bitcoins in his possession, the transfer will be successful because the universal constant has not changed. Of course, Tom will be angry because he never authorized that transaction. How can we avoid this? Signing the transactions! But this idea has two shortcomings, i) we are losing anonymity and ii) someone could impersonate an identity. Let's look at the following example:

As you can see, Bob is impersonating Alice's identity, very easy to achieve, right? However, the digital world offers an amazing advantage over the real world, in the digital world, the signature does not behave like a normal signature. A digital signature is an encryption, an algorithm that allows information to be hidden. The one that Satoshi implemented is known as ECDSA (Elliptic Curve Digital Signature Algorithm). In this article I will not discuss in detail this encryption, but instead I will give you a general idea of ​​its advantages.

Advantage 1: The transfer is anonymous

Let's consider the previous transfers but this time we will encrypt the information:

As you can see, it's impossible to determine Alice's identity. X and Y are only account numbers and the signature cannot reveal anything to us.

Advantage 2: The digital signature is unique and non-transferable

Let's consider now that Alice makes two transfers, one to Y and one to Z

As you can see, each transfer has its own digital signature, that is, it is useless to clone one signature and use it in another transfer. This implies that the digital signature (f) depends on the variable "m," where "m" is the message to be sent, e.g., "m = X sends to Y 10 BTC."

Advantage 3: The digital signature avoids double spending impersonation

Consider that Alice makes two identical transfers:

As you can see, even when "m" is the same, the generated digital signature is different. This is because "f" also depends on "#," where "#" is the transfer number, which is intrinsic to each transaction. In this sense, any attempt to double spend would not proceed, because for example, if Bob duplicates transfer #1, the digital signature would have to change and he would not be able to know it.

Advantage 4: The digital signature can be verified

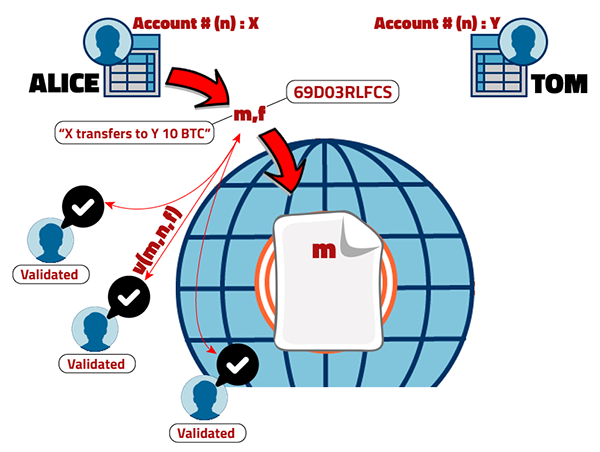
This is probably the most important advantage and it means that anyone is able to verify that the transfer is done by the right person, without knowing his real identity. It sounds paradoxical but it's just math. To understand it, you must know that every user has an account number and a password associated to it. Both are mathematically connected, and this connection is called the "public key encryption" or the "asymmetric encryption." Although a mathematical relation may imply that you can get one from the other, i.e., the password from the account number, in this case, trying to get it through algebraic steps is practically impossible, because this mathematical relation is so tough for a human to be able to solve. The account number is a public key, everyone can see it, while the password is private. Precisely, the password authenticates you as the owner and will allow you to access your personal account, therefore you must not share it with anybody. When setting a transfer, a digital signature is generated. This signature depends on the password (c) and the given message (m), that is, f(m,c). For simplicity we are ignoring "#." As you can see, if you don't have the password, you won't have the correct signature. Moreover, as seen in Fig. 4, it is the pair (m, f) that is sent to the public account but "m" is not written on the public account until "f" is validated. To validate it, a special boolean function (v) is used that depends on the account number (n), the given message (m), and the digital signature (f), that is, v(m,n,f). Interestingly, the "v" function is true only if the correct password was used, and is false in every other case. Intuitively, it makes sense because if "v" depends on "f" and "f" depends on "c," then "v" will be mathematically connected to "c," implying that if someone alters the password (or does not know it), then the "v" function will change and therefore, because it is boolean, it will output false as response.

ECDSA encryption allowed Satoshi to solve the problem of how to validate transfers while preserving anonymity; however, although Bob could no longer alter the transfers at the beginning because the correct digital signature or password is needed, he could alter them at the end, that is, when they are already registered in the public account. As you may recall, everyone has access to it, therefore nothing would prevent Bob to access the account and delete some data. What solution did Satoshi find to solve this last problem? The answer is the blockchain. To know about it, I invite you to read the third part of this article:

The blockchain