A summary of this article with some extra info appears in the following video:

In the article: "Linear extrapolation to predict the future of Despacito," published on July 11^th, 2017, making use of linear extrapolation, we correctly predicted that Despacito would reach 3 billion views on YouTube in the month of August. It officially did it on August 4^th, 2017. Despacito’s journey is shown in Table I:

In this article we answer the question: When will it reach 4 billion and 5 billion views? The answer, once again, is found in mathematics…

Since it appeared in January 2017, Despacito started to grow at a rate of 6 million views per day, then it went up to 16 million in the month of May and reached 21 million per day in the month of July. What will happen in the next few months? We forecast that by January 2018, Despacito will decline its rate to 3 million views per day because it has been the stable value of many iconic songs. Here are some examples:

How can we determine when Despacito will reach a specific number of views? To achieve this, we need to use integral calculus, which was developed by Isaac Newton and Gottfried Leibniz in the seventeenth century. Probably at that time, these geniuses had to face a similar question and that is how they developed this infinitesimal method, so let’s go back in time and imagine what they would have done. To begin with, Newton would have locked himself in his room, he was a shy person and preferred solitude. Then he would have drawn on a piece of paper a graph similar to the following:

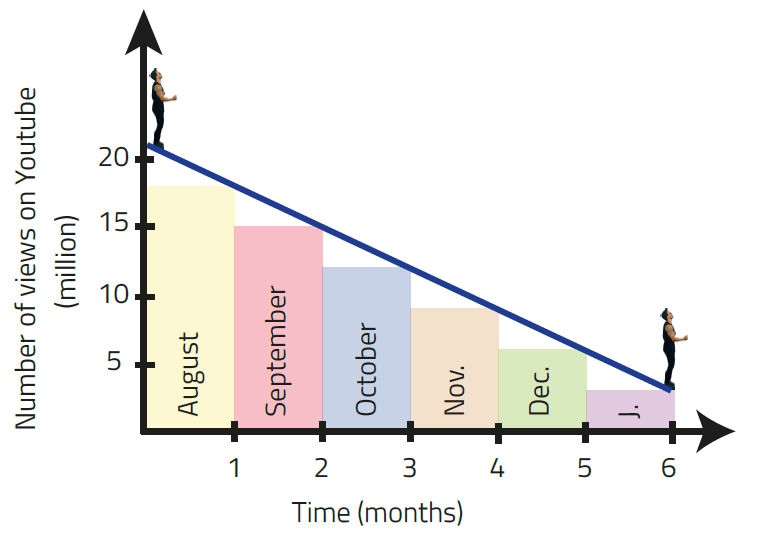
He would have shown that in 6 months (from August 2017 to January 2018) Despacito would fall linearly from 21 million to 3 million views per day (see blue line in Fig. 1), reaching a stable and constant value from then on. Why would he have done that? Because a linear trend is the simplest way to start a predictive analysis. However, even when drawing a line, calculating the date when it reaches 4 billion views seems to be a complex task.

To make it simple, Newton and Leibniz devised a trick, which consisted in drawing the rectangles given in Fig. 1. In this way we will now assume that in August, Despacito will have a constant value of 18 million views per day, in September of 15 million, in October 12 million, in November 9, in December 6, and in January 3. With this, considering that the months have either 30 or 31 days, the following table can be generated:

In Table III we are considering 26 days in the month of August. Keep in mind that officially on August 5^th, Despacito reached 3 billion views in total; therefore, it is convenient to start our calculations from August 6^th, thus giving a total of 26 days in that month. As you can see, Despacito accumulates 918 million views in the first two months (August + September), which means that it only needs 82 million more to reach the figure of 4 billion views in total. Simple calculations reveal that it would reach this number on October 7^th, 2017, because 12 x 7 days = 84 million views. Additionally, we see that from August 2017 to January 2018, Despacito accumulates 1.839 billion views, that is, a total of 4.839 billion views since January 2017, which means that it would only need 161 million to reach the figure of 5 billion views in total. Assuming that after January 2018, Despacito grows at a stable value of 3 million views per day, then in February 2018 it accumulates 3 x 28 = 84, thus 161 - 84 = 77, represents the total number of million views left to reach the figure of 5 billion views. To achieve this, only 26 days in the month March are needed, because 3 x 26 = 78; therefore, on March 26^th Despacito reaches the historical figure of 5 billion views. These results are summarized below:

The dates given in Table IV do not correspond to a solution of the blue line but instead to the approximation given by the rectangles. The funny thing is that the area of ​​each rectangle shown in Fig. 1 represents the total number of views in each month, e.g., for January, the width of the rectangle is 31 (days) and the length is 3 (number of views per day); therefore, the total number of views in that month is 31 x 3, as it appears in Table III. Oh God! — would have said the fervent Christian Newton, pulling his hair in his little room in Woolsthorpe. Leibniz would have done the same in Paris.

Both were fascinated with the concept of the infinitesimal, to the point that they were immersed in philosophical debates about the existence of monads. Because of this, at some point they wondered, what if instead of drawing monthly rectangles, we decide to draw them thinner, infinitesimally thinner so that they would exactly describe the area under the curve (the blue line in our case)? This simple thought would bring a wonderful conclusion: “The area under the curve, no matter how complicated this curve is, would give us the total number of views.”

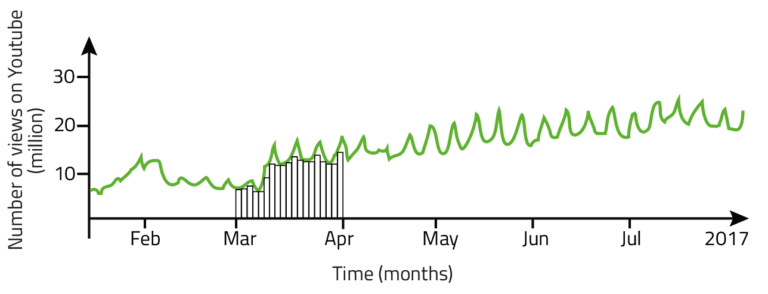
To visualize this thought, let's consider Fig. 2, where we show the evolution of the number of views of Despacito from January to August 2017. As we can see, the real behavior is not linear, but Newton and Leibniz showed us that in order to find the total number of views it was enough to find the area under the curve, in this case the area under the green line. Drawing thin rectangles in the month of March (as seen in Fig. 2) and adding their areas, would give us the total number of views in that month; however, this result is inaccurate. To achieve an accurate result we need to consider infinitesimally thin rectangles. This conclusion allowed them to develop integral calculus, which in simple words means: "To find the total area under the curve, it is enough to add the area of ​​infinitesimally thin rectangles." For this it is necessary to know the equation of our curve. In Fig. 1 is a line, whose general equation was mentioned in the article: "Linear extrapolation to predict the future of Despacito." In Fig. 2 the equation is more complex but not impossible to obtain. In this case we will focus on Fig. 1, whose linear equation is given by the function: $$f(t) = 21 - \frac{18}{178}t,$$ where $t$ represents the time, e.g., for $t=0$, that is, August 6^th, 2017, we get 21 (million). For $t=178$, that is, January 31^st, 2018, we obtain 3 (million). The function allows us to obtain the value of the rectangle's length, while the width will be given by an infinitesimally small number. Therefore, we can get the area of ​​each rectangle, what we need to do now is to add these areas up. Mathematically, this infinitesimal sum is expressed as follows:

The symbol that resembles an elongated S, i.e., $\int$, tells us that we will add the area of infinitesimally thin rectangles starting on day $0$ and finishing on day $d$, accumulating in that period a total number of $C$ million views. If we want to know the date when Despacito reaches 4 billion views in total, then $C = 1000$, and for the case of 5 billion views in total, we choose $C = 2000$. This is because day $0$ begins on August 6^th, when Despacito already reached 3 billion views. As an example, let’s solve the first case, i.e.:

This result tells us that 54.87 days after August 6^th, 2017, Despacito will reach 4 billion views. In a similar way, we obtain that 147.92 days later, Despacito will touch 5 billion views. Therefore, the final results are:

As expected, the results in Table IV and V are different. The first one is an approximation considering monthly rectangles, the second one applies integral calculus. However, the fact that the former is much more simple does not imply that the results given in Table V are more reliable. In fact, both models exhibit a margin of error because we start from a linear decay and, as we saw in Fig. 2, the behavior is actually chaotic. Then, the final conclusion could be given as a combination of the two results obtained, that is, "it reaches 4 billion views between September and October, and 5 billion views between January and April." As you may notice, we have extended the second forecast until April because a linear trend usually exhibits a greater error as we keep moving forward in time. When do you think another song would beat Despacito? Likely none in the short term, of course the great advantage that new songs have is that the global internet connection is increasing; however, if the world's population is meant to decrease for any reason, it will take many, many years for any song to surpass Despacito.